Como o raciocínio recursivo TRM prova que menos é mais

Você acha que um pequeno rede neural (como o TRM) pode superar modelos muitas vezes maiores em tarefas de raciocínio? Como é possível que bilhões de parâmetros LLM tenham um número tão pequeno de iterações modestas de um milhão de parâmetros resolvendo quebra-cabeças?

“Atualmente, vivemos em um mundo obcecado pela escala: mais dados. Mais GPUs significam modelos maiores e melhores. Este mantra impulsionou o progresso na IA até agora.”

Mas às vezes menos é realmente mais, e os Modelos Recursivos Ting (TRMs) são exemplos ousados ​​desse fenômeno. Os resultados, comprovados em este relatóriosão poderosos: os TRMs alcançam 87,4% de precisão no Sudoku-Excessive e 45% no ARC-AGI-1, enquanto excedem o desempenho de modelos hierárquicos maiores, e enquanto alguns modelos de última geração como DeepSeek R1, Claude e o3-mini pontuaram 0% no Sudoku. E DeepSeek R1 obteve 15,8% no ARC-1 e apenas 1,3% no ARC-2, enquanto um modelo TRM 7M obteve 44,6% de precisão. Neste weblog, discutiremos como os TRMs alcançam o raciocínio máximo por meio de arquitetura mínima.

A busca por modelos mais inteligentes e não maiores

Inteligência synthetic passou para uma fase dominada por modelos gigantescos. O movimento tem sido direto: basta dimensionar tudo, ou seja, surgirão dados, parâmetros, computação e inteligência.

Contudo, à medida que os investigadores e os profissionais persistem na expansão dessa fronteira, começa a surgir uma constatação. Maior nem sempre é igual a melhor. Para raciocínio estruturado, precisão e lógica gradual, modelos de linguagem maiores geralmente falham. O futuro da IA ​​pode não residir no tamanho que podemos construir, mas sim no quão inteligentes podemos pensar. Portanto, ele encontra 2 problemas principais:

O problema com o dimensionamento de grandes modelos de linguagem

Os grandes modelos de linguagem transformaram a compreensão da linguagem pure, o resumo e a geração criativa de textos. Eles aparentemente podem detectar padrões no texto e produzir fluência semelhante à humana.

No entanto, quando são incitados a envolver-se em raciocínio lógico para resolver quebra-cabeças de Sudoku ou mapear labirintos, a genialidade desses mesmos modelos diminui. Os LLMs podem prever a próxima palavra, mas isso não implica que possam raciocinar sobre o próximo passo lógico. Ao participar de quebra-cabeças como o Sudoku, um único dígito perdido invalida toda a grade.

Quando a complexidade se torna uma barreira

Subjacente a esta ineficiência está a arquitetura unilateral, ou seja, semelhante, dos LLMs; uma vez gerado um token, ele é corrigido, pois não há capacidade de corrigir um passo em falso. Um simples erro lógico no início pode estragar toda a geração, assim como uma célula incorreta do Sudoku estraga o quebra-cabeça. Assim, a expansão não garantirá estabilidade ou melhor raciocínio.

Os enormes requisitos de computação e dados tornam quase impossível para a maioria dos investigadores aceder a estes modelos. Assim, existe um paradoxo em que alguns dos sistemas de IA mais poderosos podem escrever ensaios e pintar quadros, mas são incapazes de realizar tarefas que mesmo um modelo recursivo rudimentar pode facilmente resolver.

A questão não é sobre dados ou escala; pelo contrário, trata-se de ineficiência na arquitectura e de que o intelectualismo recursivo pode ser mais significativo do que o intelecto expansivo.

Modelos de raciocínio hierárquico (GRH): um passo em direção ao pensamento simulado

O Modelo de raciocínio hierárquico (HRM) é um avanço recente que demonstrou como pequenas redes podem resolver problemas complexos através de processamento recursivo. O HRM possui duas implementações de transformadores, uma rede de baixo nível (f_L) e uma rede de alto nível (f_H). Cada passagem é executada da seguinte forma: o f_L pega a pergunta de entrada e a resposta atual, mais o estado latente, enquanto o f_H atualiza a resposta com base no estado latente. Esta é uma espécie de hierarquia de “pensamento” rápido (f_L) e mudanças “conceituais” mais lentas (f_H). Tanto f_L quanto f_H são transformadores de quatro camadas com parâmetros de aproximadamente 27M no whole.

A arquitetura do HRM treina com supervisão profunda: durante o treinamento, o HRM executa até 16 “etapas de melhoria” de geração sucessiva e calcula uma perda para a resposta a cada vez e compara os gradientes de todas as etapas anteriores. Basicamente, isso imita uma rede muito profunda, mas elimina a retropropagação completa.

O modelo possui um sinal de parada adaptativa (Q-learning) que decidirá o próximo momento em que o modelo irá treinar e quando interromper a atualização em cada questão. Com esta metodologia complicada, o HRM teve um desempenho muito bom: superou grandes LLMs em quebra-cabeças Sudoku, Maze e ARC-AGI com apenas uma pequena amostra com aprendizagem supervisionada.

Em outras palavras, o HRM demonstrou que modelos pequenos com recursão podem ter desempenho comparável ou melhor do que modelos muito maiores. No entanto, a estrutura da GRH baseia-se em múltiplas suposições sólidas. Seus benefícios surgem principalmente da alta supervisão, e não da rede dupla recursiva.

Na realidade, não há certeza de que f_L e f_H alcancem um equilíbrio em poucos passos. A GRH também adota um tipo de arquitetura de duas redes baseada em metáforas biológicas, tornando a arquitetura difícil de entender e ajustar. Finalmente, a parada adaptativa do HRM aumenta a velocidade de treinamento, mas duplica a computação.

Modelos recursivos minúsculos (TRM): redefinindo a simplicidade no raciocínio

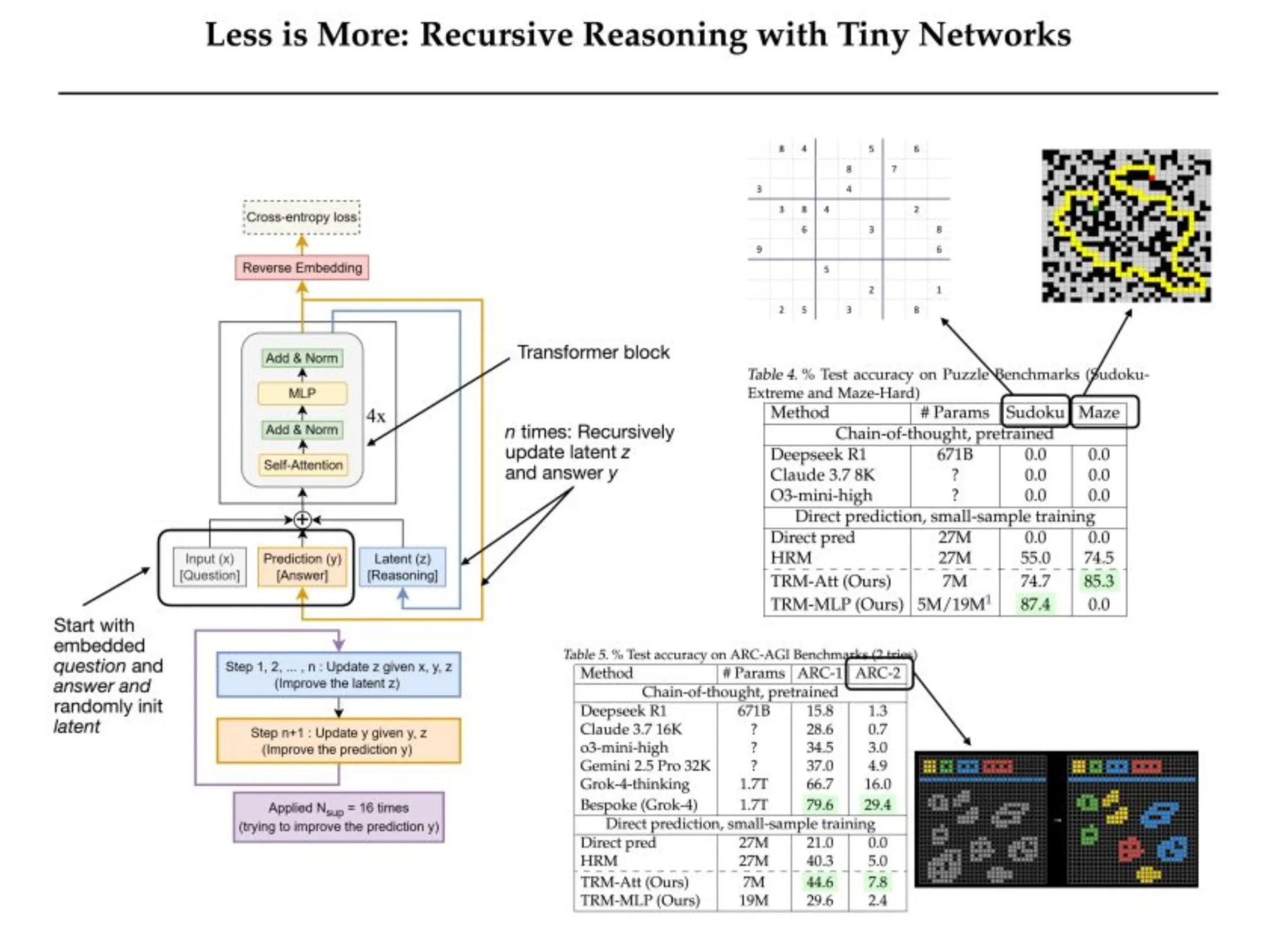
Modelos Recursivos Minúsculos (TRMs) simplificam o processo recursivo de HRMs, substituindo a hierarquia de duas redes por uma única rede minúscula. Dado um processo de recursão completo, um TRM executa este processo iterativamente e retropropaga através de toda a recursão last sem a necessidade de impor a suposição de ponto fixo. O TRM mantém explicitamente uma solução proposta 𝑦 e um estado de raciocínio latente 𝑧 e itera apenas atualizando 𝑦 e o estado de raciocínio 𝑧.

Em contraste com a instância sequencial de HRM, o loop totalmente compacto é capaz de tirar vantagem de enormes ganhos em generalização enquanto reduz os parâmetros do modelo na arquitetura TRM. A arquitetura TRM take away essencialmente a dependência de um ponto fixo e do IFT (Treinamento Implícito de Ponto Fixo), já que o PPC (Parallel Predictive Coding) é usado para o processo de recursão completo, assim como os modelos HRM. Uma única rede minúscula substitui as duas redes no HRM, o que reduz o número de parâmetros e minimiza o risco de overfitting.

Como o TRM supera modelos maiores

O TRM mantém dois estados variáveis ​​distintos, a hipótese de solução 𝑦 e a variável latente da cadeia de pensamento 𝑧. Ao manter 𝑦 separado, o estado latente 𝑧 não precisa persistir tanto o raciocínio quanto a solução explícita. O principal benefício disto é que os estados de variáveis ​​duais significam que uma única rede pode executar ambas as funções, iterando em 𝑧 e convertendo 𝑧 em 𝑦 quando as entradas diferem apenas pela presença ou ausência de 𝑥.

Ao remover uma rede, os parâmetros do HRM são cortados pela metade e precisão do modelo em tarefas-chave aumenta. A mudança na arquitetura permite que o modelo concentre seu aprendizado na iteração efetiva e reduz a capacidade do modelo onde a osmose teria se ajustado demais. Os resultados empíricos demonstram que o TRM melhora a generalização com menos parâmetros. Conseqüentemente, o TRM descobriu que menos camadas forneciam melhor generalização do que ter mais camadas. Reduzindo o número de camadas para duas, onde as etapas de recursão proporcionais à profundidade produziram melhores resultados.

O modelo é supervisionado profundamente para melhorar $y$ a verdade na hora do treinamento, em cada etapa. Ele foi projetado de tal forma que mesmo algumas passagens sem gradiente aproximarão $(y,z)$ de uma solução – portanto, aprender como melhorar a resposta requer apenas uma passagem de gradiente completa.

Benefícios do TRM

Este design é simplificado e tem muitos benefícios:

• Sem suposições de ponto fixo: O TRM elimina dependências de ponto fixo e retropropagações através de cada recursão. Executando uma série de recursões sem gradiente.
• Interpretação latente mais simples: O TRM outline duas variáveis ​​de estado: y (a solução) e z (a memória do raciocínio). Ele alterna entre refinar ambos, o que captura o pensamento para um fim e o resultado para outro. Usar exatamente esses dois, nem mais nem menos que dois, foi sem dúvida supreme para manter a clareza da lógica e ao mesmo tempo aumentar o desempenho do raciocínio.
• Rede única, menos camadas (menos é mais): Em vez de usar duas redes, como faz o modelo HRM com f_L e f_H, o TRM compacta tudo em um único modelo de 2 camadas. Isto reduz o número de parâmetros para aproximadamente 7 milhões, evita o sobreajuste e aumenta a precisão geral do Sudoku de 79,5% para 87,4%.
• Arquiteturas Específicas de Tarefas: O TRM foi projetado para adaptar a arquitetura a cada tarefa de caso. Em vez de usar duas redes, como faz o modelo HRM com f_L e f_H, o TRM compacta tudo em um único modelo de 2 camadas. Isto reduz o número de parâmetros para aproximadamente 7 milhões, evita o sobreajuste e aumenta a precisão geral do Sudoku de 79,5% para 87,4%.
• Profundidade de recursão otimizada: O TRM também emprega uma média móvel exponencial (EMA) nos pesos para estabilizar a rede. A suavização de pesos ajuda a reduzir o overfitting em dados pequenos e a estabilidade com EMA.

Resultados experimentais: modelo minúsculo, grande impacto

Modelos recursivos minúsculos demonstram que modelos pequenos podem ter desempenho superior grandes LLMs em algumas tarefas de raciocínio. Em várias tarefas, a precisão do TRM excedeu a do HRM e de grandes modelos pré-treinados:

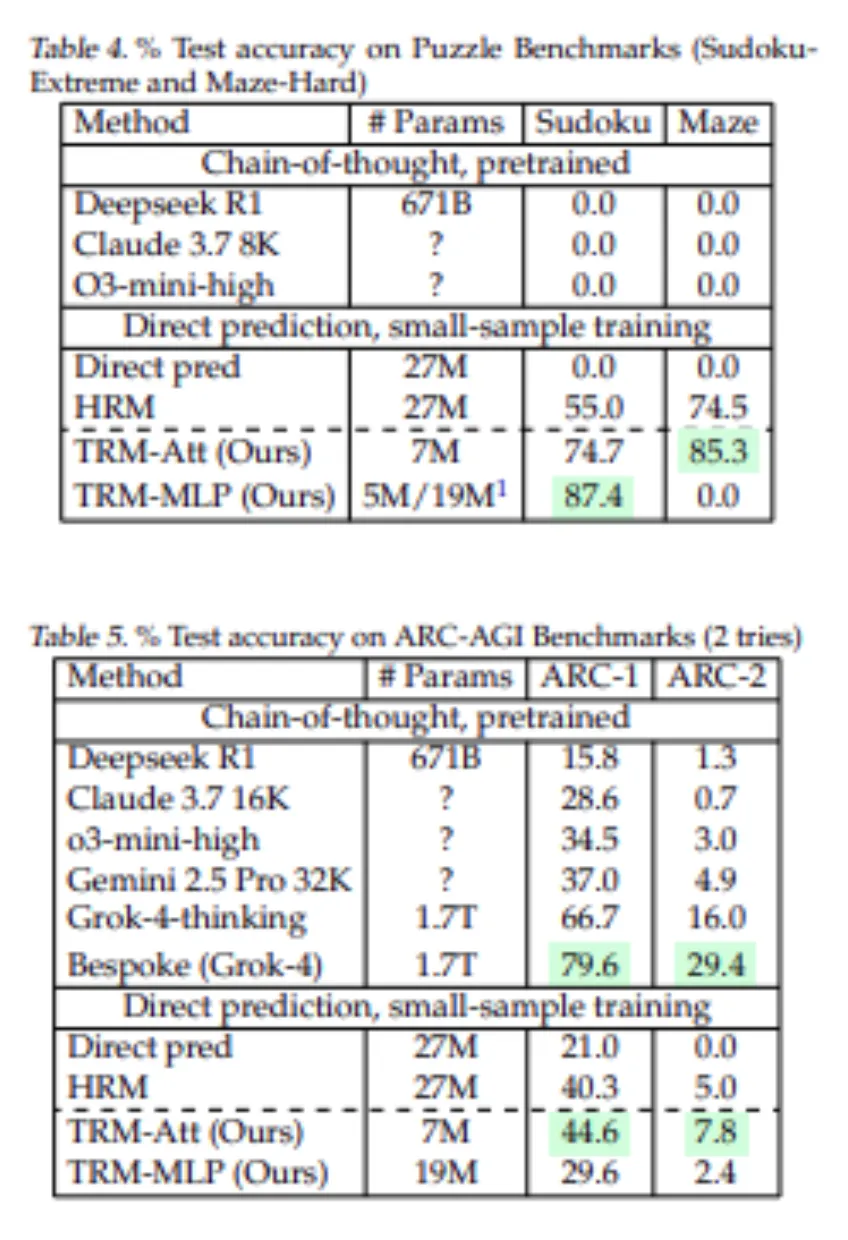
• Sudoku-Extremo: Estes são Sudokus muito difíceis. HRM (27 milhões de parâmetros) tem 55,0% de precisão. TRM (apenas 5–7 milhões de parâmetros) salta para 87,4 (com MLP) ou 74,7 (com atenção). Nenhum LLM está próximo. Os LLMs de cadeia de pensamento de última geração (Deepseek R1, Claude, o3-mini) pontuaram 0% neste conjunto de dados.
• Labirinto Difícil: Para labirintos de descoberta de caminhos com comprimento de solução> 110, o TRM com atenção é 85,3% preciso versus 74,5% do HRM. A versão MLP obteve 0% aqui, indicando que é necessária autoatenção. Novamente, LLMs treinados obtiveram aproximadamente 0% no Maze-Onerous neste regime de pequenos dados.
• ARC-AGI-1 e ARC-AGI-2: No ARC-AGI-1, TRM (7M) obteve 44,6% de precisão contra HRM 40,3%. No ARC-AGI-2, o TRM obteve 7,8% de precisão contra 5,0% do HRM. Ambos os modelos funcionam bem em comparação com um modelo de previsão direta, que é um modelo 27M (21,0% no ARC-1 e uma nova cadeia de pensamento LLM Deepseek R1 obteve 15,8% no ARC-1 e 1,3% no ARC-2). Mesmo em cálculos de tempo de teste intenso, o LLM Gemini 2.5 Professional superior obteve apenas 4,9% no ARC-2, enquanto o TRM obteve o dobro (praticamente sem dados de ajuste fino).

Conclusão

Modelos recursivos minúsculos ilustram como você pode obter habilidades de raciocínio consideráveis ​​com arquiteturas recursivas pequenas. As complexidades são eliminadas (ou seja, não há truques de ponto fixo/uso de redes duplas, nem camadas densas). O TRM fornece resultados mais precisos e usa menos parâmetros. Utiliza metade das camadas e condensa duas redes e possui apenas alguns mecanismos simples (EMA e um mecanismo de parada mais eficiente).

Essencialmente, o TRM é mais simples que o HRM, mas generaliza muito melhor. Este artigo mostra que pequenas redes bem projetadas com aprendizado recursivo, profundo e supervisionado pode realizar o raciocínio com sucesso em problemas difíceis sem atingir um tamanho enorme.

No entanto, os autores colocam algumas questões em aberto para consideração, por exemplo, por que exatamente a recursão ajuda muito mais? Por que não criar uma rede feedforward maior, por exemplo?

Por enquanto, o TRM é um exemplo poderoso de arquiteturas de IA eficientes, pois pequenas redes superaram os LLMs em quebra-cabeças lógicos e demonstram que às vezes menos é mais no aprendizado profundo.

Olá! Sou Vipin, um entusiasta apaixonado por ciência de dados e aprendizado de máquina, com uma sólida base em análise de dados, algoritmos de aprendizado de máquina e programação. Tenho experiência prática na construção de modelos, gerenciamento de dados confusos e solução de problemas do mundo actual. Meu objetivo é aplicar insights baseados em dados para criar soluções práticas que gerem resultados. Estou ansioso para contribuir com minhas habilidades em um ambiente colaborativo enquanto continuo aprendendo e crescendo nas áreas de Ciência de Dados, Aprendizado de Máquina e PNL.